引言

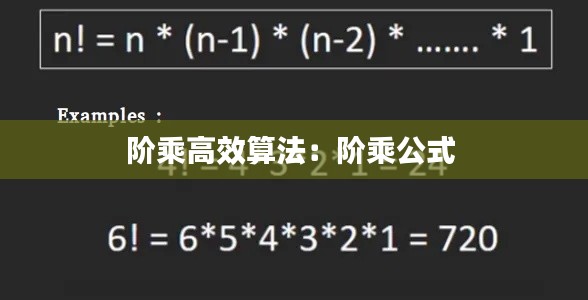
阶乘是一个数学概念，表示一个正整数n的阶乘，记作n!，是指从1乘到n的所有整数的乘积。例如，5! = 5 × 4 × 3 × 2 × 1 = 120。阶乘在数学、计算机科学、统计学等领域都有广泛的应用。然而，随着n的增大，阶乘的计算会变得非常缓慢。因此，研究阶乘的高效算法具有重要的实际意义。

常规阶乘算法

最简单的阶乘算法是通过循环从1乘到n来实现的。这种算法的时间复杂度为O(n)，在n不是特别大时，计算效率是可以接受的。但是，当n增大时，这种算法的运行时间会显著增加。以下是一个简单的Python代码实现常规阶乘算法：

def factorial(n):
    result = 1
    for i in range(1, n + 1):
        result *= i
    return result

# 示例
print(factorial(5))  # 输出120

递归阶乘算法

递归是另一种实现阶乘的方法。递归阶乘算法基于这样一个事实：n! = n × (n-1)!。递归算法可以简化代码，但需要注意的是，递归阶乘算法在n非常大时可能会遇到栈溢出的问题。以下是一个使用递归的Python代码实现：

def factorial_recursive(n):
    if n == 0 or n == 1:
        return 1
    else:
        return n * factorial_recursive(n - 1)

# 示例
print(factorial_recursive(5))  # 输出120

阶乘的高效算法

为了提高阶乘计算的效率，我们可以采用一些优化策略。以下是一些常用的阶乘高效算法：

使用动态规划

动态规划是一种通过存储中间结果来避免重复计算的方法。我们可以使用一个数组来存储从1到n的所有阶乘值，这样在计算n!时，只需要计算n-1!的值即可。以下是一个使用动态规划的Python代码实现：

def factorial_dynamic(n):
    if n == 0 or n == 1:
        return 1
    else:
        dp = [1] * (n + 1)
        for i in range(2, n + 1):
            dp[i] = dp[i - 1] * i
        return dp[n]

# 示例
print(factorial_dynamic(5))  # 输出120

使用数学公式

阶乘的数学公式可以帮助我们减少乘法操作的次数。例如，对于两个连续的阶乘值，我们可以使用以下公式进行计算：n! = n × (n-1)! = n × (n-1) × (n-2)!。我们可以利用这个公式来减少乘法操作的次数。以下是一个使用数学公式的Python代码实现：

def factorial_formula(n):
    result = 1
    for i in range(n, 1, -1):
        result *= i
    return result

# 示例
print(factorial_formula(5))  # 输出120

总结

阶乘的高效算法是计算机科学中的一个重要问题。通过使用动态规划、数学公式等方法，我们可以显著提高阶乘计算的效率。在实际应用中，选择合适的算法取决于具体的需求和数据的规模。了解这些算法可以帮助我们在处理大规模数据时更加高效地完成计算任务。